Bombaz Bass Synth

Bombaz is an electronic bass VSTi based on the little-known technique of window function synthesis. This plug-in is particularly useful for adding sub-bass layers as it produces more harmonics than a simple sine wave.

In this blog post I’ll explain the synthesis method used. You can grab the code and VST3/AU files from GitHub.

Window function synthesis

I first learned about window function or WF synthesis from Curtis Roads’ excellent book The Computer Music Tutorial — the second edition is out now, you should get it!

The idea is very simple: For every period of a waveform you output a short pulse in the shape of a Blackman-Harris window, followed by zeros known as the deadtime.

Changing the pitch of the sound is done by using a different amount of deadtime to shorten or lengthen the period. The width of the pulse is unrelated to the pitch and only affects the timbre of the sound.

Repeating any kind of signal N times per second gives a tone of N Hz. If that signal is a sine wave, the sound contains a single harmonic. Since our signal is more complex than a pure sine wave, we get additional harmonics. The shape of the pulse determines the amplitudes of these harmonics.

In the original paper, The Efficient Digital Implementation of Subtractive Music Synthesis by Bass and Goeddel (1981), they set the width of the pulse to 8 samples, creating an impulse train that is semi-bandlimited.

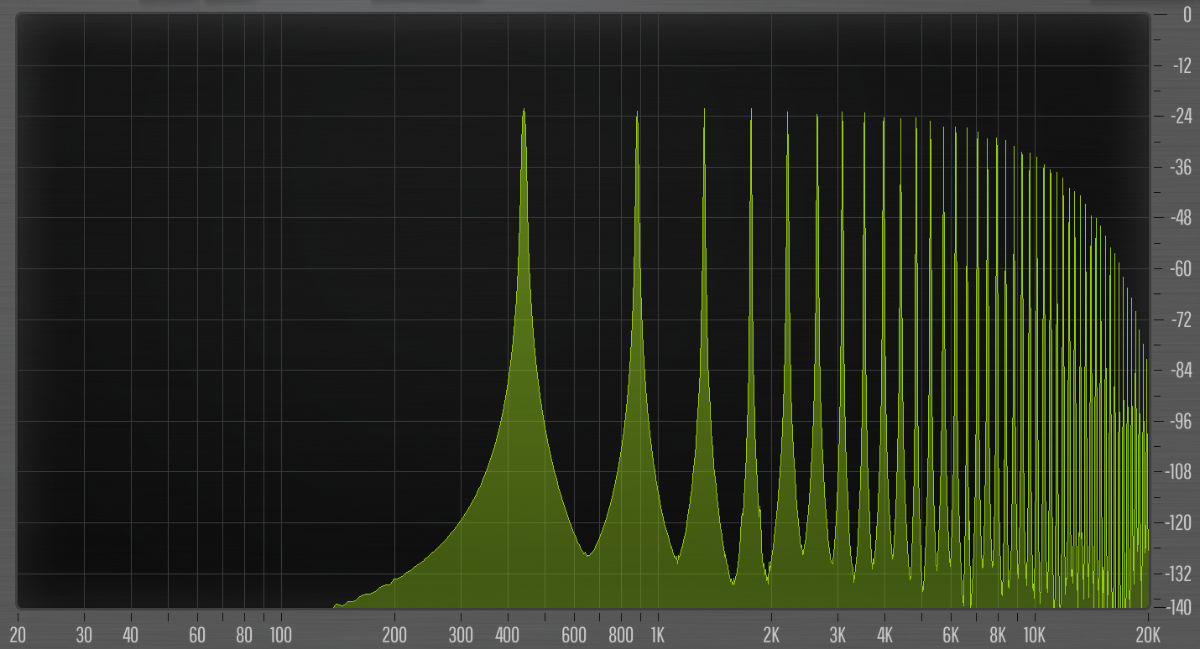
This is similar to what you get with the BLIT algorithm but simpler because there’s no need to blend together overlapping sinc pulses. The downside is roll-off at the high end, which BLIT doesn’t have. This roll-off is caused by the main lobe of the Blackman-Harris window, which now acts as a low-pass filter.

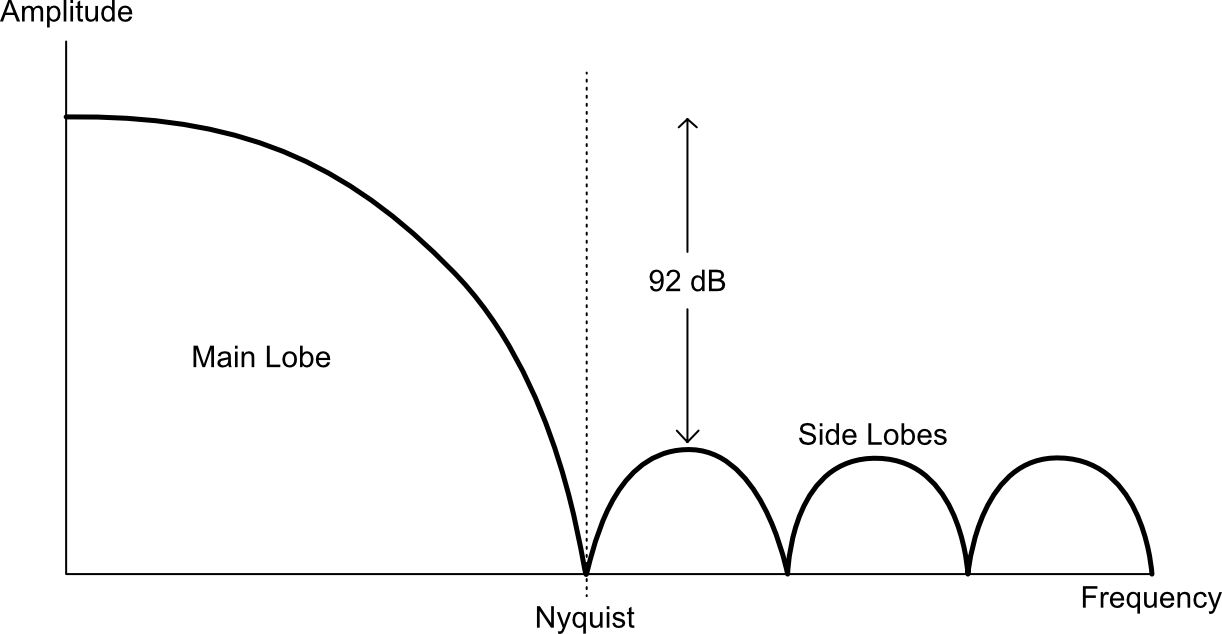
Like any windowing function, the spectrum of the Blackman-Harris window contains a main lobe and multiple sidelobes. The width of the window determines how far the main lobe extends into the spectrum. Using an 8-sample pulse, the main lobe goes all the way up to Nyquist. The sidelobes will then lie beyond Nyquist, which creates aliasing.

Blackman-Harris was chosen specifically for this synthesis method because its sidelobes are at least 92 dB below the peak of the main lobe, making these aliases inaudible. We can therefore conveniently ignore them.

Window functions were not originally intended for this purpose, and the whole thing is really a clever trick to generate a harmonically rich spectrum with only tiny amounts of aliasing. (Just like with BLIT, the resulting pulsetrain can be turned into a sawtooth by integrating it, if you were so inclined.)

There is more to WF synthesis than I’m showing here. Generating the pulsetrain is just the first step in their formant synthesis process. The formants are created by additional filtering of this harmonically rich waveform — but I’m not using any of that in Bombaz.

Implementing it “wrong”

When I first started playing with WF synthesis, I didn’t realize that they specifically fixed the width of the Blackman-Harris pulse to be 8 samples in order to get harmonics all the way up to Nyquist. Instead, I wrongly assumed the pulse width would be varied and so I hooked it up to a plug-in parameter.

I found that using a relatively long window combined with a low pitch gives the oscillator a really nice bass sound. It produces clean harmonics with a roll-off that’s different than with a regular low-pass filter. That’s how the idea for this plug-in was born.

You’ve seen that the window’s main lobe acts as a low-pass filter. The width of the pulse determines where the cutoff frequency is. A very wide pulse gives a low cutoff that filters out most of the harmonics; a narrow pulse leaves more harmonics in the sound. By varying the pulse width we get different timbres that sound quite sweet at low frequencies.

A happy accident! I didn’t really understand what I was doing and ended up with something that sounded cool anyway. I’m sure this happens a lot in audio development. 😅

The oscillator

Let’s look at class Oscillator where the WF synthesis stuff happens. The source code for this plug-in is on GitHub in case you want to look at the entire thing.

At start of a new period the oscillator outputs the Blackman-Harris pulse, followed by zeros until the next period starts. For efficiency reasons, the pulse is read from a 1024-element wavetable. I’m using the four-term Blackman-Harris window from the following formula:

$$ w(t) = 0.35875 - 0.48829 \cos(2 \pi t / N) + 0.14128 \cos(4 \pi t / N) - 0.01168 \cos(6 \pi t / N) $$

Reading from the wavetable uses a simple linear interpolation. There is some noise in the spectrum at the high end due to the interpolation but it’s inaudible. Because the spectrum of the Blackman-Harris window has sidelobes there’s lots of crap at the high end anyway, but it’s so quiet that it doesn’t matter.

The output waveform is described by the following properties:

• Pitch: This determines how long the waveform’s period is. To change pitch, simply add a different amount of deadtime after the pulse.

• Pulse width: How wide the Blackman-Harris window is decides the amount of low-pass filtering — the wider the window, the lower the cutoff.

• Amplitude: The height of the pulse. In this synth there is no velocity so all notes are equally loud. However, we do need to vary the amplitude to get equal perceived loudness between different notes.

The oscillator’s code for computing the next sample value is as follows.

float nextSample() noexcept
{
    float output = 0.0f;

    // 1
    if (pos < size) {
        output = readFromWavetable(pos);
        output *= amplitude;

        pos += inc;  // 2
    }

    // 3
    phase += 1.0f;
    if (phase >= period) {  // 4
        phase -= period;
        pos = phase * inc;

        applyChanges();  // 5
    }

    return output;
}

What this does step-by-step:

1. Output the pulse by playing through the wavetable once. pos is the position in the wavetable; size is the length of the wavetable. If pos < size, we’re still rendering the pulse. Otherwise, output silence.

2. At every sample timestep, pos is incremented. The speed by which we step through the wavetable is given by inc. A larger inc means a shorter pulse.

3. The period variable contains the length of one full cycle in samples. phase counts how far along we are in the current cycle.

4. When we’re done with this period, restart the wavetable so that we’ll start outputting a new pulse again on the next cycle.

5. Also after each period the function applyChanges() is called. If any of the waveform properties changed — pitch, pulse width, amplitude — the new values are only applied at the start of the next period.

The advantage of waiting until the new period to apply changes in the parameters is that we don’t need an envelope for attack/release and we don’t need to smoothen any of our parameters — because changes are always applied when they can’t cause glitches.

Playing an E2 note (82.4 Hz) with the pulse width parameter at its longest setting, which corresponds to a pulse length of 15 milliseconds, gives the following spectrum:

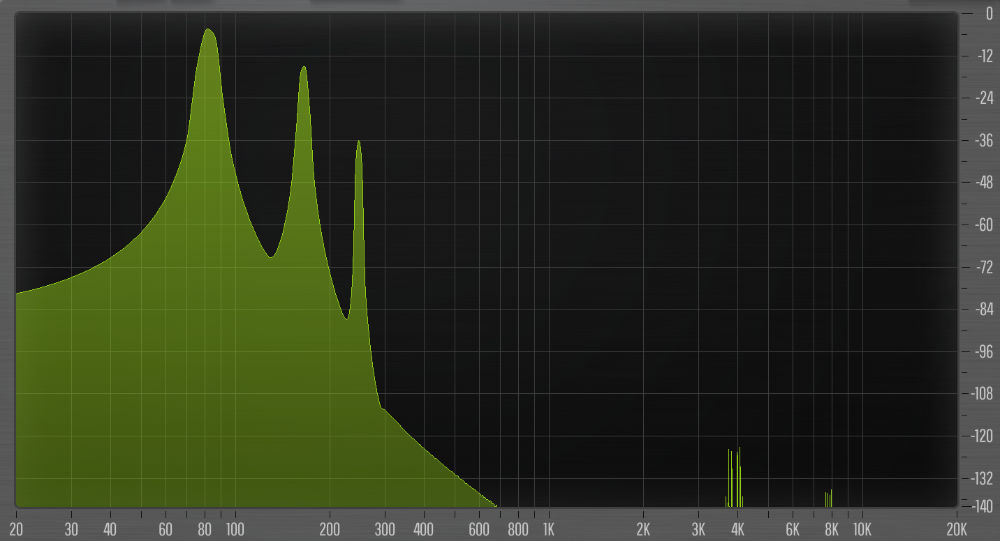
The same note with pulse width at its shortest setting (3 milliseconds) looks like this:

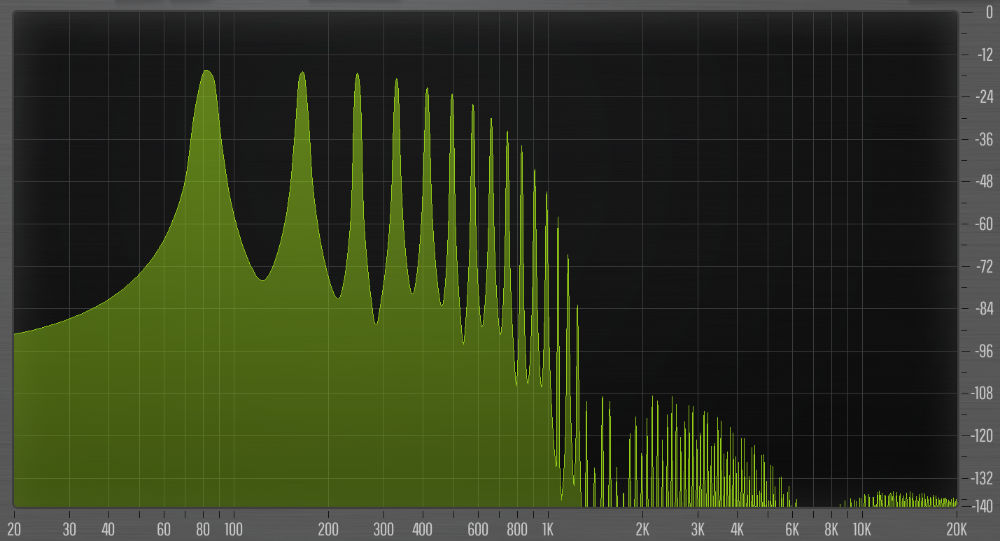
It’s clear that the shorter pulse creates a much richer spectrum. Personally I prefer a sound that’s somewhere in the middle of these two extremes. Notice that in the second image the sidelobes are clearly visible but are below –100 dB.

The reason I said this plug-in was great for adding sub-bass is that it produces a fat sound with more harmonics than just a plain sine wave. The way the harmonics roll off gives the WF oscillator a unique timbre.

DC killer

Since the window function pulses are always positive, there is a DC component in the sound. It’s not a big deal because the signal always returns to zero, but I figured adding a DC-blocking filter would be useful anyway. This is a simple one-pole high-pass filter.

The waveform before the DC killer:

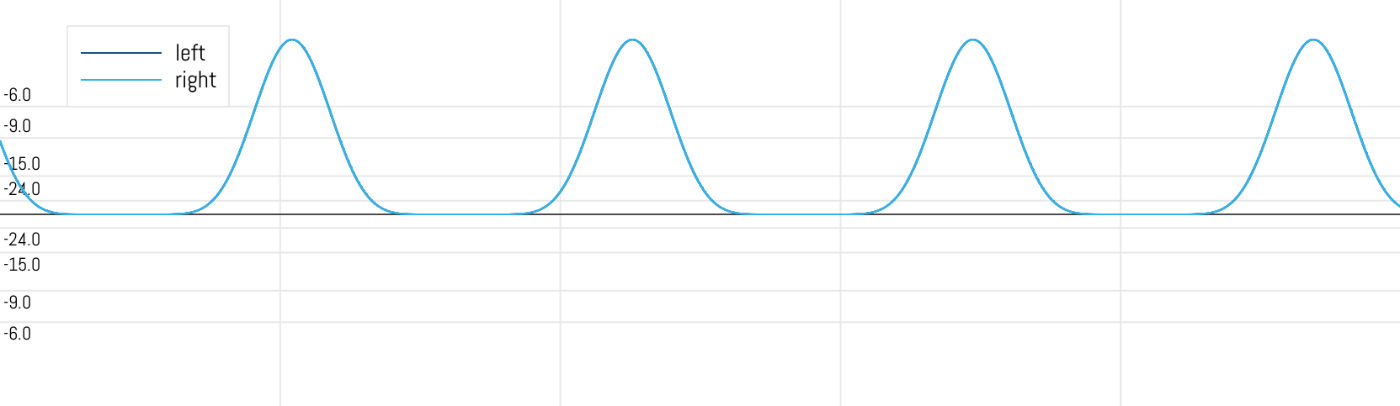
With the DC killer applied:

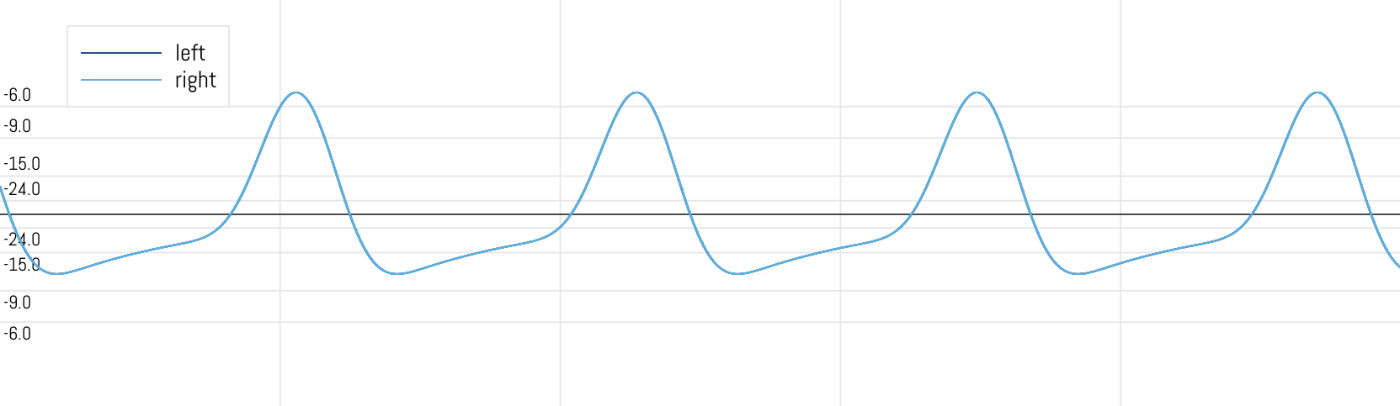
A nice benefit is that it reduces the maximum amplitude of the signal so that we can push the gain a little more. Plus it hides the fact that we’re using WF synthesis, and makes the waveforms look cooler. 😆

Loudness compensation

Ideally, all notes should be equally loud. But with my WF oscillator there are two things that affect loudness:

1. The pitch of the note. A lower note has a longer period and therefore more deadtime (silence) than higher notes with shorter periods. Thus, high notes appear louder than low notes.

2. The pulse width. The DC killer pulls the signal down, so that longer pulses have a lower amplitude than short pulses.

Because lower notes with more deadtime sound quieter, so we compensate for this by reducing the amplitude of higher notes. I did some experiments and came up with the following formula:

float f = std::clamp(pitch, 27.5f, 440.0f);
compensation = 1.0f - 0.2f * std::log2(f / 27.5f);

The compensation variable is 1.0 at a frequency of 27.5 Hz or lower. Every higher octave reduces this by 0.2, so that 55 Hz = 0.8, 110 Hz = 0.6, 220 Hz = 0.4, and 440 Hz = 0.2. This more-or-less gives the same RMS at all these frequencies.

However, this is not enough by itself. Longer pulse widths have a lower amplitude because of the DC killer. We compensate for this by boosting by 3 dB at the longest pulse width (15 milliseconds) down to 0 dB for the shortest pulse (3 milliseconds).

float dB = (pulseTime - 0.003f) * 250.0f;
compensation *= decibelsToGain(dB);

The compensation value is then multiplied into the amplitude of the pulse.

Drive

The WF oscillator already sounds quite interesting by itself. However, I wanted to add some extra distortion to the sound. After trying a few methods, I decided on using the first half of the Blackman-Harris window as a waveshaper, since that has a gentle sigmoid-like shape, followed by basic atan soft-clipping.

You’ve already seen the oscillator’s nextSample() function but I left out the distortion part. The full function does the following when reading from the wavetable:

if (pos < size) {
    output = readFromWavetable(pos);

    // Use half the Blackman-Harris window as waveshaper.
    wet = readFromWavetable(output * size * 0.5f);
    output += drive * 0.8f * (wet - output);

    // Soft-clipping waveshaper.
    wet = std::atan(k * output) * oneOverAtanK;
    output += drive * (wet - output);

    output *= amplitude;
    pos += inc;
}

Here, drive is hooked up to a plug-in parameter, and the other variables are derived from it inside the applyChanges() function:

k = drive*5.0f + 1.0f;
oneOverAtanK = 1.0f / std::atan(k);

Waveshaping generally aliases like crazy but for bass notes most of the harmonics don’t get anywhere near Nyquist, so it’s no problem. You will see some aliasing when playing higher notes, but why would you?!

In the UI, the Pulse Width and Drive parameters are combined into an XY pad, so that you can vary both at the same time to dial in just the sound you like.

Glide

To wrap up this blog post, I quickly want to mention how I implemented glide. The logic for this happens in the Voice class.

Voice’s pitch variable holds the current pitch of the oscillator. When a new note starts, the target variable is set to the pitch of that new note. If the user is playing legato-style, meaning that the previous key is still being held down, we do the following:

float semitones = semitonesBetweenFrequencies(pitch, target);
if (semitones != 0.0f) {
    glide = std::exp2(semitones / (12.0f * params.glideTime));
    glideDir = (glide > 1.0f) ? 1.0f : -1.0f;
    target *= glideDir;
}

This calculates a multiplier glide based on the glide time set by the user and by how many semitones the target is away from the current pitch. If glide is greater than 1, the sound will go up in pitch; if less than 1, the pitch is going down. The variable glideDir also keeps track of this direction, to avoid having to branch later.

The reason for using the distance in semitones is that the glide will now be performed using a constant speed, from beginning to end. Often glide is imlemented using a one-pole filter, which is fast in the beginning and then slows down, but I like the constant speed version better.

In the voice’s render() function we then do:

if (glide != 1.0f) {
    pitch *= glide;
    if (pitch * glideDir >= target) {
        pitch = target * glideDir;
        glide = 1.0f;
    }
}
osc.setPitch(pitch);
return osc.nextSample();

If gliding is active, this first updates pitch to move it closer to the target. Once the target has been reached, we turn off gliding again.

Even though we potentially update pitch on every sample timestep, recall that the new pitch isn’t used until the next period. There’s no need to smoothen the glide time parameter because changes to the pitch don’t take effect until the oscillator begins the next waveform cycle, and so there is no zipper noise.

All right, enough talking. Now go play with this synth! 🎶